本章将会详细讲解二叉树遍历的四种方式，分别为前序遍历、中序遍历、后续遍历和层序遍历。

在学习遍历之前，会先带大家回顾一下二叉树的基本概念。学习二叉树的基本操作前，

需要先创建一颗二叉树，然后才能学习其相关的基本操作，考虑到我们刚刚接触二叉树，

为了能够先易后难地进行讲解，我们将暂时手动创建一颗简单的二叉树，用来方便大家学习。

等二叉树结构了解的差不多后，后期我们会带大家研究二叉树地真正的创建方式。

1.二叉树概念

复习链接：

比特数据结构与算法（第四章_上）树和二叉树和堆的概念及结构_GR C的博客-CSDN博客

二叉树是什么？① 空树 ② 非空：根节点、根节点的左子树与根节点的又子树组成的。

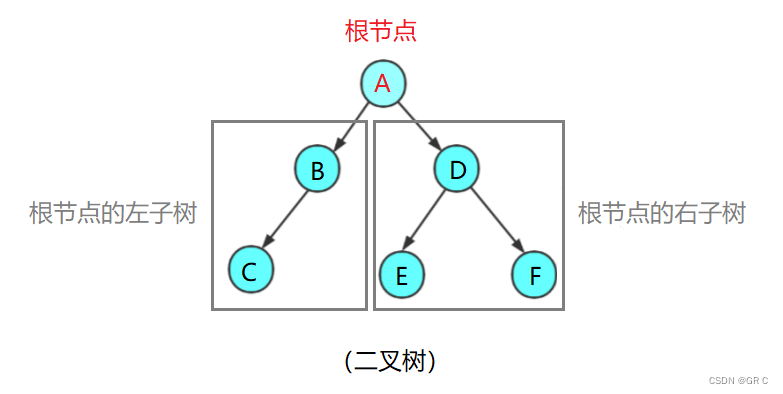
解读：从概念中我们不难看出，二叉树的定义是递归式的。因此后续基本操作中，

我们基本都是按照该概念来实现的！我们可以来看一下，我们不去看 A，我们来看 A 的左子树，

把 B 看作为根节点，又是颗二叉树。

所以，我们可以通过采用递归的手法来实现二叉树。

2.二叉树定义

#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>typedef int BTDataType;typedef struct BinaryTreeNode 
{struct BinaryTreeNode* left;       // 记录左节点struct BinaryTreeNode* right;      // 记录右节点BTDataType data;                   // 存储数据
} BTNode;//创建新节点
BTNode* CreateNode(BTDataType x) 
{BTNode* new_node = (BTNode*)malloc(sizeof(BTNode));if (new_node == NULL){printf("malloc failed!\n");exit(-1);}new_node->data = x;new_node->left = new_node->right = NULL;return new_node;
}//手动创建二叉树 
BTNode* CreateBinaryTree() 
{BTNode* nodeA = CreateNode('A');BTNode* nodeB = CreateNode('B');BTNode* nodeC = CreateNode('C');BTNode* nodeD = CreateNode('D');BTNode* nodeE = CreateNode('E');BTNode* nodeF = CreateNode('F');nodeA->left = nodeB;         //           AnodeA->right = nodeC;        //       B        CnodeB->left = nodeD;         //    D        E    FnodeC->left = nodeE;       nodeC->right = nodeF;        return nodeA;
}int main(void)
{BTNode* root = CreateBinaryTree();
}

3.二叉树深度优先遍历

学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历，就是按照某种特定的规则，一次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。 访问节点所做的操作要看具体的应用问题。遍历是二叉树上最重要的运算之一，也是二叉树上进行其他运算的基础。

二叉树遍历（Traversal）：沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。 按照规则，二叉树的遍历有：前序 / 中序 / 后序 的递归结构遍历。除了前序、中序和后续遍历外，我们还可以对二叉树进行层序遍历。

比如二叉树的中序遍历：

3.1二叉树前序遍历

前序遍历（Preorder Traversal）：访问根节点的操作发生在遍历其右子树之前。

即，首先访问根结点，然后遍历左子树，最后遍历右子树。

代码实现前序遍历：

//二叉树前序遍历
void PreOrder(BTNode* root)
{//首先判断根是否为空，为空就返回if (root == NULL){printf("NULL ");    // 暂时打印出来，便于观察       return;}//走到这里说明不为空，根据前序遍历，先访问根节点printf("%c ", root->data);//然后遍历左子树（利用递归）PreOrder(root->left);//最后遍历右子树（利用递归）PreOrder(root->right);//           A//       B        C//    D        E    F        前序：根 左 右//执行输出：  A B D NULL NULL NULL C E NULL NULL F NULL NULL
}

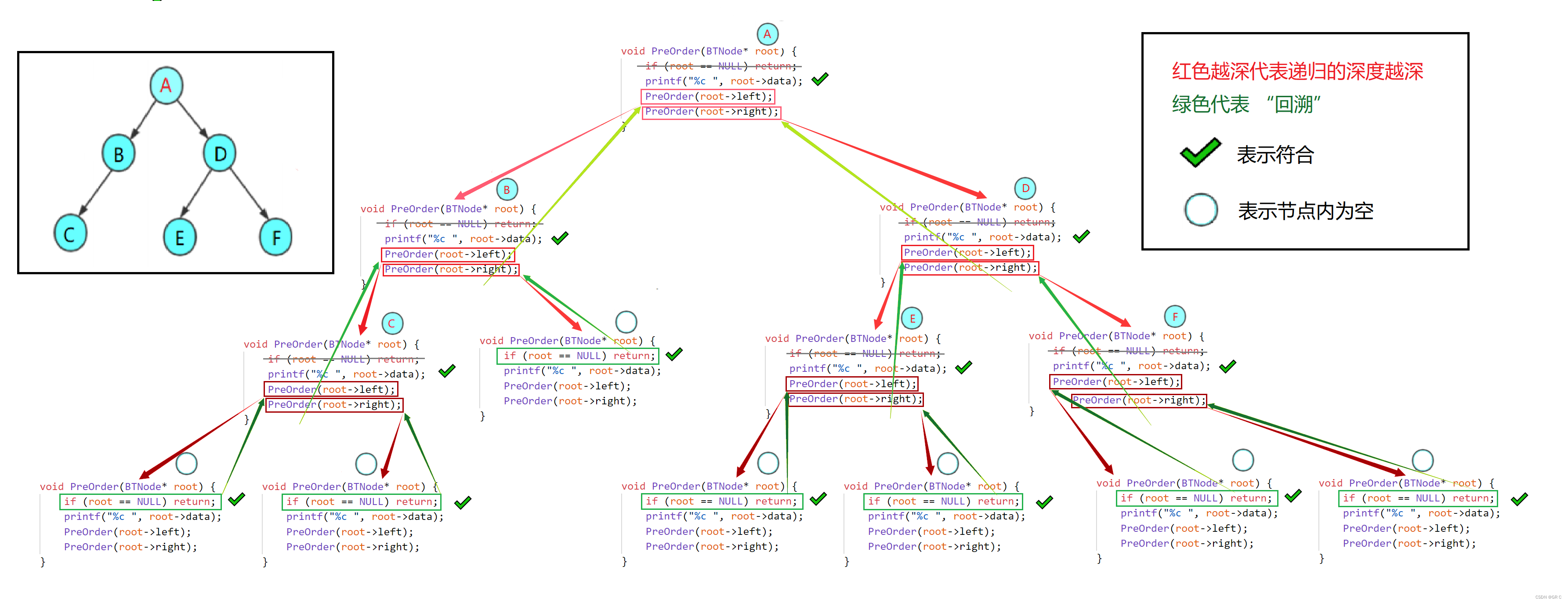
① 首先判断根是否为空，如果根为空，则返回。这里为了表示，我们把空节点以 " Ø " 打印出来。

② 如果跟不为空，这说明有数据。由于是前序遍历（Preorder），前序遍历是先访问根节点，然后遍历左子树，最后再遍历右子树。所以，我们这里先要访问的是根节点，我们把根节点的数据打印出来。

③ 然后我们需要遍历左子树，这时我们利用递归就可以实现。将根节点 root 的左数 left 传入 PreOrder 函数（将其左树看作根），一直递归下去，直到碰到 root == NULL 则返回。

④ 最后，遍历完左子树后遍历右子树。利用递归，方法同上。

3.2二叉树中序遍历

递归的中序和后序和前序差不多 顺序换一下就行

//二叉树中序遍历
void InOrder(BTNode* root) 
{if (root == NULL) {printf("NULL ");  return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);//           A//       B        C//    D        E    F         中序：左  根  右//执行输出：NULL D NULL B NULL A NULL E NULL C NULL F NULL
}

3.3二叉树后序遍历

void PostOrder(BTNode* root) 
{if (root == NULL) {printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);//           A//       B        C//    D        E    F        后序：左  右  根//执行输出：NULL NULL D NULL B NULL NULL E NULL NULL F C A
}

3.4二叉树深度优先遍历完整代码：

#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>typedef int BTDataType;typedef struct BinaryTreeNode 
{struct BinaryTreeNode* left;       // 记录左节点struct BinaryTreeNode* right;      // 记录右节点BTDataType data;                   // 存储数据
} BTNode;//创建新节点
BTNode* CreateNode(BTDataType x) 
{BTNode* new_node = (BTNode*)malloc(sizeof(BTNode));if (new_node == NULL){printf("malloc failed!\n");exit(-1);}new_node->data = x;new_node->left = new_node->right = NULL;return new_node;
}//手动创建二叉树 
BTNode* CreateBinaryTree() 
{BTNode* nodeA = CreateNode('A');BTNode* nodeB = CreateNode('B');BTNode* nodeC = CreateNode('C');BTNode* nodeD = CreateNode('D');BTNode* nodeE = CreateNode('E');BTNode* nodeF = CreateNode('F');nodeA->left = nodeB;         //           AnodeA->right = nodeC;        //       B        CnodeB->left = nodeD;         //    D        E    FnodeC->left = nodeE;       nodeC->right = nodeF;        return nodeA;
}
//二叉树前序遍历
void PreOrder(BTNode* root)
{//首先判断根是否为空，为空就返回if (root == NULL){printf("NULL ");    // 暂时打印出来，便于观察       return;}//走到这里说明不为空，根据前序遍历，先访问根节点printf("%c ", root->data);//然后遍历左子树（利用递归）PreOrder(root->left);//最后遍历右子树（利用递归）PreOrder(root->right);//           A//       B        C//    D        E    F        前序： 根 左 右//执行输出：  A B D NULL NULL NULL C E NULL NULL F NULL NULL
}//二叉树中序遍历
void InOrder(BTNode* root) 
{if (root == NULL) {printf("NULL ");  return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);//           A//       B        C//    D        E    F        中序：左 根 右//执行输出：NULL D NULL B NULL A NULL E NULL C NULL F NULL
}//二叉树后序遍历
void PostOrder(BTNode* root) 
{if (root == NULL) {printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);//           A//       B        C//    D        E    F        后序：左  右  根//执行输出：NULL NULL D NULL B NULL NULL E NULL NULL F C A
}
int main()
{BTNode* root = CreateBinaryTree();PreOrder(root);printf("\n");InOrder(root);printf("\n");PostOrder(root);
}

4.二叉树广度优先遍历

4.1层序遍历

层序遍历（Level Traversal）：设二叉树的根节点所在的层数为1的情况下，

从二叉树的根节点出发，首先访问第1层的树根节点，然后再从左到右访问第2层上的节点。

接着是第3层的节点……以此类推，自上而下、从左向右地逐层访问树的节点。

该如何实现层序遍历呢？ 我们可以利用队列的性质来实现！

我们之前再讲过队列，这里你可以选择自己实现一个队列。

如果不想实现就直接复制即可，因为我们这里重点要学的是层序遍历！

链接：比特数据结构与算法（第三章_下）队列的概念和实现（力扣：225+232+622）_GR C的博客-CSDN博客

本篇完。

下一篇写写二叉树的OJ题，二叉树就暂时结束了